Elementary Mathematics - Computation Strategies
| In the elementary grades, a major focus of students' work is becoming fluent with addition, subtraction, multiplication, and division. In mathematics, the word fluent means "accurate, efficient, and flexible." Students develop fluency in each operation through several years of careful development that includes practice of facts and procedures as well as activities that deepen understanding and flexibility. Developing fluency is "not a matter of instilling facts and procedures divorced from their meanings, but rather an outcome of a multi-year process that heavily involves the interplay of practice and reasoning." (Progression for CC and OA (draft), pp. 18 – 19; http://commoncoretools.me/category/progressions/) |
Progression of Addition Strategies Leading to the Standard Algorithm
|
Drawing Tens & Ones |
Adding in Expanded Notation |
U.S. Standard Algorithm in Expanded Notation |
U.S. Standard Algorithm |
|
|
|
|
|
|
This strategy is used in grades 1 and 2 to provide a visual model for both addition and subtraction. After drawing the tens and ones for each addend, some students will count on from 45, beginning 55, 65, 75, then counting on by ones. Other students will combine ones to make a 10, viewing 5 ones and 8 ones as 1 ten and 3 ones. This strategy helps build conceptual understanding of the operations and it evoloves into strategies that are more efficient for larger numbers. |
Students should be able to use this strategy by the end of grade 2. Adding using expanded notation helps build understanding of place value and allows students to write all of their calculations without regrouping (a.k.a., ‘carrying’), which makes it easier for students to understand. |
Students should be able to use this strategy by the end of grade 3. It still uses expanded notation to build place value understanding, but introduces regrouping (a.k.a., ‘carrying’) in a way that is easy to understand in order to prepare students to transition to the U.S. Standard Algorithm.
Students should be able to do this before they begin to transition to the U.S. Standard Algorithm.
|
This strategy is required in grade 4 by standard 4.NBT.4. It follows a very similar set of steps as the strategy shown to the left, but uses a more compact notation to make it more efficient. This efficiency, however, also obscures the place value of the numbers and the logic of the steps (ex., after adding 5 tens + 6 tens, a student breaks apart the 11 tens, writing a ‘1’ at the bottom of the tens place and another ‘1’ (rather than ‘10’) at the top of the hundreds place). Students will come to understand the logic of each step and the meaning of the shorthand much better when they follow the progression of strategies depicted here. Therefore, this algorithm should not be introduced prematurely. |
Progression of Subtraction Strategies Leading to the Standard Algorithm
|
Direct Modeling |
Drawing Tens & Ones |
U.S. Standard Algorithm in Expanded Notation |
U.S. Standard Algorithm |
|
|
|
|
|
|
This strategy is used in grades K and 1 to provide a visual model for subtraction. Students model the original number (minuend) and then cross off the quantity indicated (subtrahend). Note that most subtraction work in kindergarten is within 10; in grade 1, it is within 20. This example was provided to highlight the efficiency of drawing the minuend in rows of 10 ones and crossing off an entire row, when appropriate. Developmentally, most children cannot ‘unitize’ (see 10 ones as a ten) until grade 1. |
Students should be able to use this strategy by the end of grade 2. It is still concrete/pictorial, but more efficient than the strategy shown to the left. This strategy helps develop place value understanding as students draw tens and ones and builds on students knowledge of pairs that make 10 (learned in kindergarten) as they decide how to break-up a 10 to do the subtraction. |
Students should be able to use this strategy by the end of grade 3. It uses expanded notation to build understanding of place value and regrouping (a.k.a., trading or borrowing) in a way that is easy to understand. Students should be able to do this before they begin to transition to the U.S. Standard Algorithm. |
This strategy is required in grade 4 by standard 4.NBT.4. It follows a very similar set of steps as the strategy shown to the left, but uses a more compact notation to make it more efficient. This efficiency, however, also obscures the place value of the numbers and the logic of the steps (ex., after regrouping, it is hard for students to see that we still have 832). Students will come to understand the logic of each step and the meaning of the shorthand much better when they follow the progression of strategies depicted here. Therefore, this algorithm should not be introduced prematurely. |
Grade 3 Progression of Multiplication Strategies
(scroll down to see strategies for grades 4 & 5)
|
Circles and Stars |
Area Model |
Partial-Products |
|
|
|
|
|
This is a good visual model for multiplication and division. This picture shows 4 groups of 16. This strategy is intended to help build a conceptual understanding of multiplication / division, but it is not efficient for larger numbers. Students must transition to one of the other two strategies on this progression before the end of grade 3. |
This strategy is required in third grade. It depicts standard 3.MD.7, where students break apart one of the factors by place value and multiply each part by the other factor (using the distributive property). The area of the whole rectangle is equal to the sum of each of the partial areas, showing that area "is additive." Students must be able to do this by the end of grade 3. |
Like the Area Model, this strategy uses the distributive property. Students multiply one factor by each place value of the other factor; then add the "partial-products" together. This is a more abstract representation of the exact same steps shown in the Area Model and a more concrete representation of the exact steps used in the U.S. Standard Algorithm.
All students will master this strategy in grade 4, but those who are ready for a more abstract strategy should be encouraged to use this one in grade 3. |
Grades 4 & 5 Progression of Multiplication Strategies
|
Area Model |
Partial-Products |
U.S. Standard Algorithm |
|
|
|
|
|
This strategy provides a good visual model for multiplication, relating it to the process for finding the area of a rectangle. The visual model helps ensure that students remember to multiply every digit of one factor by every digit of the other factor (using the distributive property). |
Like the Area Model, this strategy uses the distributive property. Students multiply every digit of one factor by every digit of the other factor; then add the "partial-products" together. This is a more abstract representation of the exact same steps shown in the Area Model and a more concrete representation of the exact steps used in the U.S. Standard Algorithm.
Students should be able to do this by the end of grade 4. |
This strategy is required in fifth grade by standard 5.NBT.5. It follows the exact same steps as Partial-Products, but uses a more compact notation to make it more efficient. This efficiency, however, also obscures the place value of the numbers and the logic of the steps. Students will come to understand the logic of each step and the meaning of the shorthand much better when they follow the progression depicted here. Therefore, this algorithm should not be introduced prematurely. Students must be able to do this by the end of grade 5. |
Grades 3 - 5 Progression of Division Strategies
|
Circles and Stars |
Partial-Quotients |
Partial-Quotients |
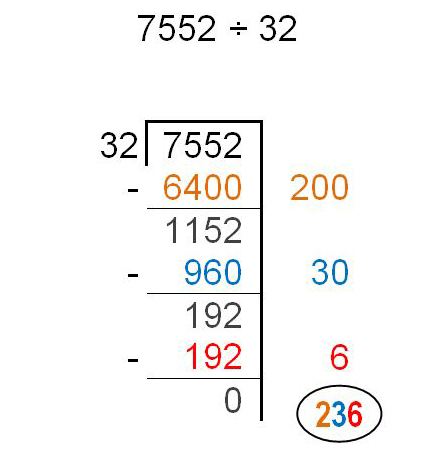
U.S. Standard Algorithm |
|
Click on the picture above to see a 3rd grader explain this strategy.
|
Click on the picture above to see a 4th grader explain this strategy.
|
 Click on the picture above to see a 4th grader explain this strategy.
|
Click on the picture above to see a 5th grader explain this strategy. |
|
This strategy is used in grade 3 to provide a visual model for both multiplication and division as they are first being introduced. The picture shows 64 being split into 4 equal groups. (The student first gives 10 to each circle (40 altogether). With 24 left to split, the student gives 5 more to each circle, after which 60 have been split among the four circles. Finally one more is given to each circle, so 64 have been split equally.) This strategy helps build a conceptual understanding of the operations, but it is not efficient for larger numbers. |
This strategy is used in grade 4. It is a modified version of the U.S. Standard Algorithm that allows students to write all of their calculations and maintains place value at each step, making it easier for students to understand. This is a more abstract representation of the exact same steps shown in Circles and Stars, but not yet as efficient (or abstract) as the U.S. Standard Algorithm.
By the end of grade 4, students should be able to do each place value in one step (shown in the next column). |
When students maximize the efficiency of this strategy (use only one partial-quotient for each place value), this strategy becomes as compact and efficient as the U.S. Standard Algorithm. To do it, a student thinks: “Can at least one hundred 32’s fit into 7552? Yes, that would be 3200. Will two hundred 32’s fit? Yes, that’s 6400. Will three hundred 32’s fit? No, that’s too big.” This thought process is followed for each place value.
Students should be able to do this (with only one partial-quotient for each place value) before they begin to transition to the U.S. Standard Algorithm. |
This strategy is required by the standards in grade 6 (6.NS.2), though it is taught in grade 5 at Skaneateles. It follows a very similar set of steps as Partial-Quotients, but uses a more compact notation to make it more efficient. This efficiency, however, also obscures the place value of the numbers and the logic of the steps (ex., A student thinks “How many 32’s are in 75?” rather than 7500.). Students will come to understand the logic of each step and the meaning of the shorthand much better when they follow the progression of strategies depicted here. Therefore, this algorithm should not be introduced prematurely. |
